TypeScript实现二叉搜索树-灵析社区
前言
树是一种非顺序数据结构,它用于存储需要快速查找的数据。现实生活中也有许多用到树的例子,比如:家谱、公司的组织架构图等。
本文将详解二叉搜索树并用TypeScript将其实现,欢迎各位感兴趣的开发者阅读本文。
实现思路
二叉树中的节点最多只能有两个子节点:一个是左侧子节点, 另一个是右侧子节点。
二叉搜索树是二叉树的一种,它与二叉树的不同之处:
- 每个节点的左子节点一定比自身小
- 每个节点的右子节点一定比自身大
本文主要讲解树的具体实现,不了解树基础知识的开发者请移步: 数据结构: 二叉查找树
二叉搜索树的实现
根据二叉搜索树的特点我们可知: 每个节点都有2个子节点,左子节点一定小于父节点,右子节点一定大于父节点。
创建辅助类Node
首先,我们需要一个类来描述二叉树中的每个节点。由二叉树的特点可知,我们创建的类必须包含如下属性:
- key 节点值
- left 左子节点的引用
- right 右子节点的引用
和链表一样,我们将通过指针来表示节点之间的关系,在双向链表中每个节点包含两个指针, 一个指向下一个节点,两一个指向上一个节点。树也采用同样的方式(使用两个指针), 但是树的指针一个指向左子节点,另一个指向右子节点。
下图描述了一个二叉树, 节点与节点之间的链接就是指针。
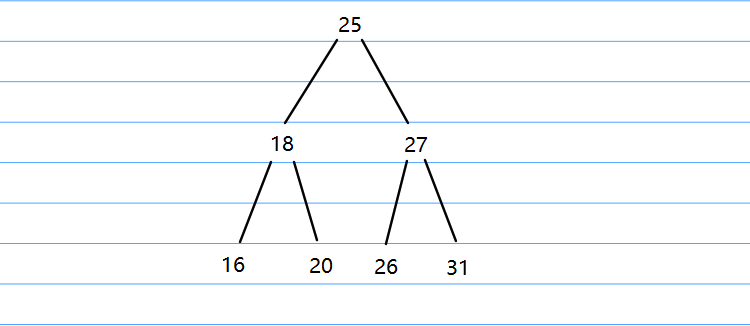
创建二叉搜索树的基本结构
我们采用与链表相同的做法,通过声明一个变量来控制此数据结构的第一个节点(根节点), 在树中此节点为root。
接下来,我们来分析下实现一个二叉搜索树都需要实现的方法:
- insert(key): 向树中插入一个节点
- search(key): 在树中查找一个键。如果节点存在返回true, 否则返回false
- min(): 返回树中最小的值 / 键
- max(): 返回书中最大的值 / 键
- remove(key): 从树中移除某个键
向树中插入一个新的节点
- 验证插入操作是否为特殊情况: 根节点为null, 如果根节点为null则创建一个Node类的实例并将其赋值给root属性,将root指向新创建的节点
- 如果根节点不为null, 则需要寻找合适的位置来插入子节点, 因此我们需要实现一个辅助方法insertNode
- insertNode方法接收两个参数: 要从哪里开始插,要插入节点的key
- 由于二叉搜索树有一个特点是: 左子节点小于父节点, 右字节点大于父节点。所以我们需要创建一个比对方法compareFn
- compareFn方法接收两个参数: 要比对的值,原值。如果小于则返回-1, 如果大于则返回1, 相等则返回0
- 调用compareFn方法判断要插入的键是否小于当前节点的键
- 如果小于, 判断当前节点的左子节点是否为null, 如果为null则创建Node节点将其指向左子节点, 否则从当前节点的左子节点位置开始递归调用insertNode方法,寻找合适的位置
- 如果大于, 判断当前节点的右子节点是否为null, 如果为null则创建Node节点将其指向右子节点,否则从当前节点的右子节点位置开始递归调用 insertNode方法, 寻找合适的位置
接下来,我们通过一个例子来描述下上述过程。
我们要将下述数据插入二叉树中:30 21 25 18 17 35 33 31
- 首先,插入30,此时根节点为null,创建一个Node节点将其指向root
- 然后,插入21,此时比较21和30的大小,21 < 30。在30的左子节点插入, 30的左子节点为null。因此直接插入
- 然后,插入25 < 30,在30的左子节点插入,此时30的左子节点已经有了21,递归调用insertNode,比较25和21的大小,25 > 21,因此在21的右子节点插入
- 依此类推,直至所有节点都插入。
搜索树中的值
在树中,有三种经常执行的搜索类型:
- 搜索最小值
- 搜索最大值
- 搜索特定的值
接下来,我们通过一个例子来描述下搜索特定的值的过程。
如下图所示为一个二叉搜索树,我们需要判断25是否在树中:
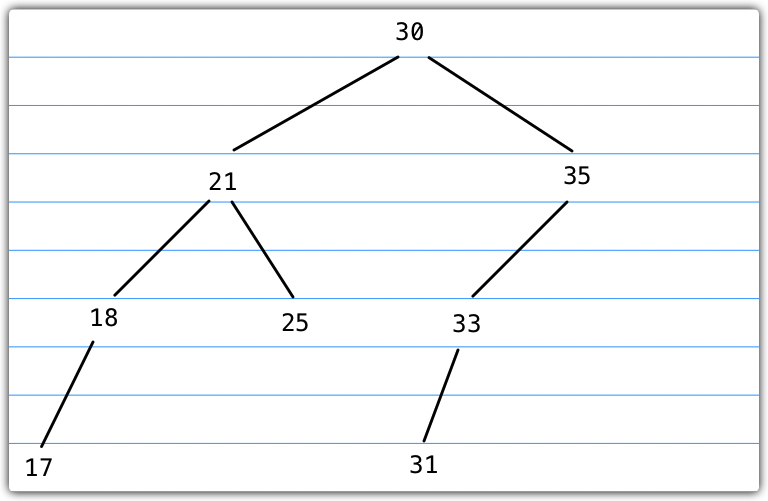
- 调用search方法,要查找的键为25,调用searchNode方法,需要从根节点开始找,因此传root和要查找的key
- 首先,node不为空,则继续判断key与根节点键的大小,25 < 30,递归它的左子树
- 然后,比较25和21的大小,25 > 21,递归它的右子树
- 此时,25 === 21,节点已找到,返回true
移除一个节点
移除树中的节点remove,它接收一个参数key,它需要一个辅助方法removeNode,它接收两个参数:节点,要移除的key。
removeNode实现思路如下:
- 首先,判断节点是否为null,如果是则证明节点不存在返回null
- 调用compareFn方法,比较要删除的key与当前节点key的大小
- 如果要删除的key小于当前节点key,则递归调用removeNode方法,传当前节点的左子节点和key
- 如果要删除的key大于当前节点key,则递归调用removeNode方法,传当前节点的右子节点和key
- 否则就是找到了要删除的节点,删除节点可能出现三种情况:
二叉搜索树的遍历
遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程,访问树的所有节点有三种方式:
- 中序遍历
- 先序遍历
- 后序遍历
树的遍历采用递归的形式访问,对递归不了解的开发者请移步:递归的理解与实现
中序遍历
中序遍历是一种上行顺序访问树节点的遍历方式,即从小到大的顺序访问所有节点。中序遍历的一种应用场景就是对树进行排序操作,接下来我们来分析下中序遍历的实现:
- 声明inOrderTraverse方法接收一个回调函数作为参数,回调函数用来定义我们对遍历到的每个节点进行的操作,中序遍历采用递归实现,因此我们需要一个辅助方法inOrderTraverseNode
- inOrderTraverseNode方法接收两个参数:节点,回调函数
- 递归的基线条件node==null
- 递归调用inOrderTraverseNode方法,传当前节点的左子节点和回调函数
- 调用回调函数
- 递归调用inOrderTraverseNode方法,传当前节点的右子节点和回调函数
接下来,我们通过一个例子来描述下中序遍历的过程
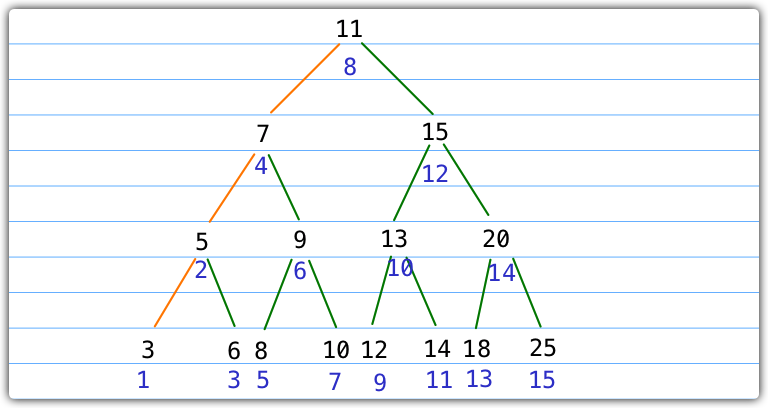
如上图所示,蓝色字标明了节点的访问顺序,橙色线条表示递归调用直至节点为null然后执行回调函数。
具体的执行过程如下:
11=>7=>5=>3
ode:3,
left:undefined
callback(node.key) 3
right:undefined
allback(node.key) 5
node:5,
right:6
left:undefined
callback(node.key) 6
right: undefined
callback(node.key) 7
node:7,
right:9
left:8
left:undefined
callback(node.key) 8
right:undefined
callback(node.key) 9
right:10
left:undefined
callback(node.key) 10
right:undefined
allback(node.key) 11
node:11,
right:15
left:13
left:12
left:undefined
callback(node.key) 12
right:undefined
callback(node.key) 13
right:14
left:undefined
callback(node.key) 14
right:undefined
...... ...
right:25
left:undefined 25
callback(node.key)
先序遍历
先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构化的文档,接下来我们分析下先序遍历的具体实现:
- 声明preOrderTraverse方法,接收的参数与中序遍历一样,它也需要一个辅助方法preOrderTraverseNode
- preOrderTraverseNode方法接收的参数与中序遍历一样
- 递归的基线条件: node == null
- 调用回调函数
- 递归调用preOrderTraverseNode方法,传当前节点的左子节点和回调函数
- 递归调用preOrderTraverseNode方法,传当前节点的右子节点和回调函数
接下来,我们通过一个例子来描述下先序遍历的过程:
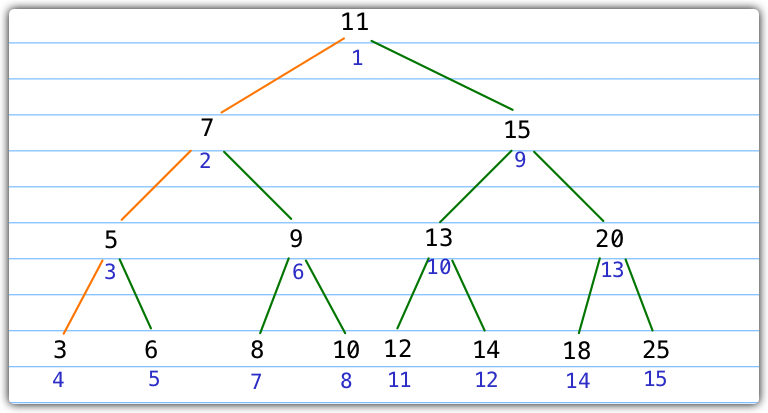
如上图所示,蓝色字标明了节点的访问顺序,橙色线表示递归调用直至节点为null然后执行回调函数。
具体的执行过程如下:
node:11
callback(node.key) 11
node.left=7
ode:7
callback(node.key) 7
node.left=5
ode:5
callback(node.key) 5
ode.left=3
node:3
callback(node.key) 3
node.left=undefined,node.right=undefined => node:5
node:5
node.right = 6
callback(node.key) 6
node:6
node.left=undefined,node.right=undefined => node:7
node:7
node.right = 9
callback(node.key) 9
...... ...
callback(node.key) 25
后序遍历
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目录及其子目录中所有文件所占空间的大小,接下来我们来分析下后序遍历的实现:
- 声明postOrderTraverse方法,接收的参数与中序遍历一致
- 声明postOrderTraverseNode方法,接收的参数与中序遍历一致
- 递归的基线条件为node == null
- 递归调用postOrderTraverseNode方法,传当前节点的左子节点和回调函数
- 递归调用postOrderTraverseNode方法,传当前节点的右子节点和回调函数
- 调用回调函数
接下来,我们通过一个例子来描述下后序遍历的执行过程。
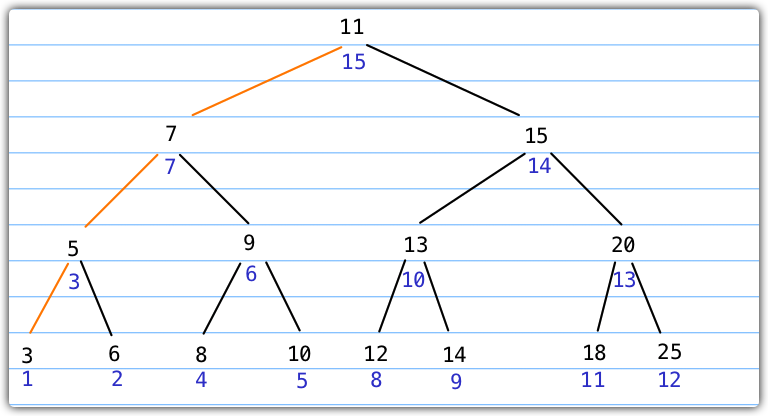
如上图所示,蓝色字标示了节点的执行顺序,橙色线表示递归调用直至节点为null然后执行回调函数。
具体的执行过程如下:
11=>7=>5=>3
node:3
left:undefined
right:undefined
callback(node.key) 3
node:5
right:6
ode:6
left:undefined
right:undefined
callback(node.key) 6
node:5
callback(node.key) 5
node:7
right: 9
node:9
left:8
node:8
left:undefined
right:undefined
callback(node.key) 8
node:9
right:10
node:10
left:undefined
right:undefined
callback(node.key) 10
node:9
callback(node.key) 9
node:7
callback(node.key) 7
... ...
callback(node.key) 11
实现代码
前面我们分析了二叉搜索树的实现思路,接下来我们就讲上述思路转换为代码。
创建辅助节点
- 创建Node.ts文件
- 创建Node类,根据节点的属性为类添加对应属性
export class Node<K> {
public left: Node<K> | undefined;
public right: Node<K> | undefined;
constructor(public key: K) {
this.left = undefined;
this.right = undefined;
}
toString() {
return `${this.key}`;
}
}
完整代码请移步: Node.ts
创建二叉树的基本结构
- 创建BinarySearchTree.ts文件
- 声明root节点和比对函数
protected root: Node<T> | undefined;
constructor(protected compareFn: ICompareFunction<T> = defaultCompare) {
this.root = undefined;
};
export type ICompareFunction<T> = (a: T, b: T) => number;
export function defaultCompare<T>(a:T, b:T) {
if (a === b){
return Compare.EQUALS;
}else if(a > b) {
return Compare.BIGGER_THAN;
}else {
return Compare.LESS_THAN;
}
}
- 实现节点插入
insert(key: T){
if (this.root == null){
// 如果根节点不存在则直接新建一个节点
this.root = new Node(key);
}else {
// 在根节点中找合适的位置插入子节点
this.insertNode(this.root,key);
}
}
protected insertNode(node: Node<T>, key: T) {
// 新节点的键小于当前节点的键,则将新节点插入当前节点的左边
// 新节点的键大于当前节点的键,则将新节点插入当前节点的右边
if (this.compareFn(key,node.key) === Compare.LESS_THAN){
if (node.left == null){
// 当前节点的左子树为null直接插入
node.left = new Node(key);
}else {
// 从当前节点(左子树)向下递归,找到null位置将其插入
this.insertNode(node.left,key);
}
}else{
if (node.right == null){
// 当前节点的右子树为null直接插入
node.right = new Node(key);
}else {
// 从当前节点(右子树)向下递归,找到null位置将其插入
this.insertNode(node.right,key);
}
}
}
- 获取节点的最大值、最小值以及特定节点
// 搜索特定节点的值
search(key: T){
return this.searchNode(<Node<T>>this.root, key);
}
private searchNode(node: Node<T>, key: T): boolean | Node<T>{
if (node == null){
return false;
}
if (this.compareFn(key, node.key) === Compare.LESS_THAN){
// 要查找的key在节点的左侧
return this.searchNode(<Node<T>>node.left, key);
} else if(this.compareFn(key, node.key) === Compare.BIGGER_THAN){
// 要查找的key在节点的右侧
return this.searchNode(<Node<T>>node.right, key);
} else{
// 节点已找到
return true;
}
}
// 获取树的最小节点
min(){
return this.minNode(<Node<T>>this.root);
}
protected minNode(node: Node<T>): Node<T>{
let current = node;
while (current != null && current.left != null){
current = current.left;
}
return current;
}
// 获取树的最大节点
max(){
return this.maxNode(<Node<T>>this.root);
}
private maxNode(node: Node<T>){
let current = node;
while (current != null && current.right != null){
current = current.right;
}
return current;
}
- 实现节点移除
remove(key: T){
this.removeNode(<Node<T>>this.root,key);
}
protected removeNode(node: Node<T> | null, key: T){
// 正在检测的节点为null,即键不存在于树中
if (node == null){
return null;
}
// 不为null,需要在树中找到要移除的键
if (this.compareFn(key,node.key) === Compare.LESS_THAN){ // 目标key小于当前节点的值则沿着树的左边找
node.left = <Node<T>>this.removeNode(<Node<T>>node.left, key);
return node;
} else if (this.compareFn(key,node.key) === Compare.BIGGER_THAN){ // 目标key大于当前节点的值则沿着树的右边找
node.right = <Node<T>>this.removeNode(<Node<T>>node.right, key);
return node;
} else{
// 键等于key,需要处理三种情况
if (node.left == null && node.right == null){ // 移除一个叶节点,即该节点没有左、右子节点
// 将节点指向null来移除它
node = null;
return node;
}
if (node.left == null){ // 移除一个左侧子节点的节点
// node有一个右侧子节点,因此需要把对它的引用改为对它右侧子节点的引用
node = <Node<T>>node.right;
// 返回更新后的节点
return node;
} else if(node.right == null){ // 移除一个右侧子节点的节点
// node有一个左侧子节点,因此需要把对它的引用改为对它左侧子节点的引用
node = node.left;
// 返回更新后的节点
return node;
}
// 移除有两个子节点的节点
const aux = this.minNode(node.right); // 当找到了要移除的节点后,需要找到它右边子树最小的节点,即它的继承者
node.key = aux.key; // 用右侧子树最小的节点的键去更新node的键
// 更新完node的键后,树中存在了两个相同的键,因此需要移除多余的键
node.right = <Node<T>>this.removeNode(node.right, aux.key) // 移除右侧子树中的最小节点
return node; // 返回更新后的节点
}
}
二叉树的遍历
接下来我们实现中序、先序、后序遍历
- 实现中序遍历
inOrderTraverse(callback: Function){
this.inOrderTraverseNode(<Node<T>>this.root,callback);
}
private inOrderTraverseNode(node: Node<T>,callback: Function){
if (node !=null){
this.inOrderTraverseNode(<Node<T>>node.left,callback);
callback(node.key);
this.inOrderTraverseNode(<Node<T>>node.right,callback);
}
}
- 实现先序遍历
preOrderTraverse(callback: Function){
this.preOrderTraverseNode(<Node<T>>this.root, callback);
}
private preOrderTraverseNode(node: Node<T>, callback: Function){
if (node != null){
callback(node.key);
this.preOrderTraverseNode(<Node<T>>node.left, callback);
this.preOrderTraverseNode(<Node<T>>node.right, callback);
}
}
- 实现后序遍历
postOrderTraverse(callback: Function){
this.postOrderTraverseNode(<Node<T>>this.root, callback);
}
private postOrderTraverseNode(node: Node<T>, callback: Function) {
if (node != null){
this.postOrderTraverseNode(<Node<T>>node.left, callback);
this.postOrderTraverseNode(<Node<T>>node.right, callback);
callback(node.key);
}
}
完整代码请移步: BinarySearchTree.ts
编写测试代码
前面我们实现了二叉搜索树以及它的基本方法,接下来我们来测试下上述代码是否都能正常执行。
const binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(11);
binarySearchTree.insert(7);
binarySearchTree.insert(15);
binarySearchTree.insert(5);
binarySearchTree.insert(3);
binarySearchTree.insert(9);
binarySearchTree.insert(8);
binarySearchTree.insert(10);
binarySearchTree.insert(13);
binarySearchTree.insert(12);
binarySearchTree.insert(14);
binarySearchTree.insert(20);
binarySearchTree.insert(18);
binarySearchTree.insert(25);
binarySearchTree.insert(6);
// 测试中序遍历函数
const printNode = (value) => console.log(value);
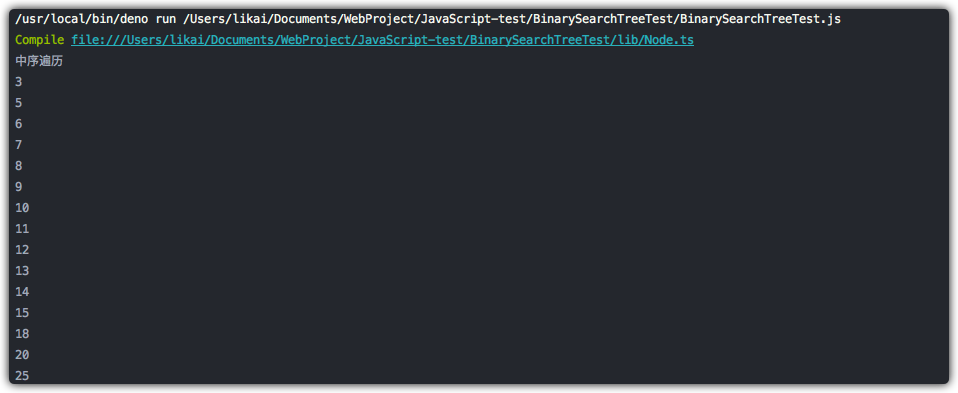
console.log("中序遍历");
binarySearchTree.inOrderTraverse(printNode);
// 测试先序遍历
console.log("先序遍历");
binarySearchTree.preOrderTraverse(printNode);
// 测试后序遍历
console.log("后序遍历");
binarySearchTree.postOrderTraverse(printNode);
// 测试获取最小值函数
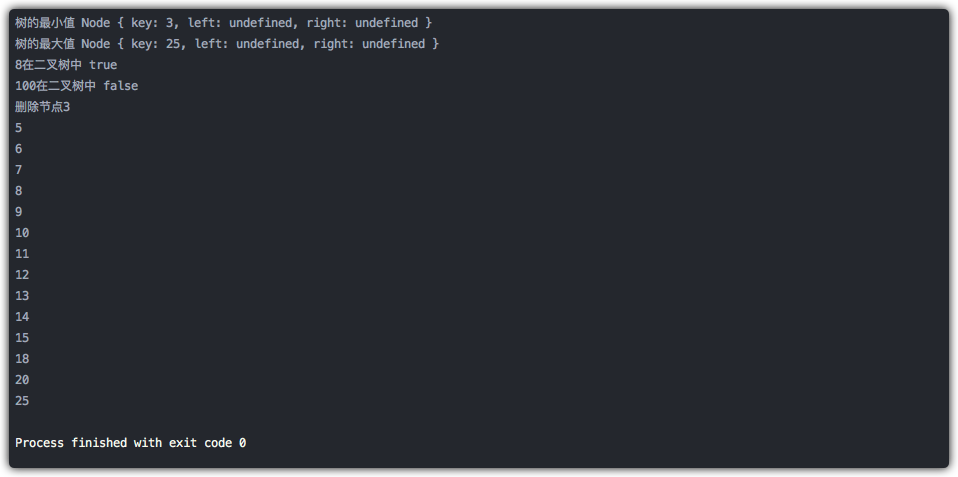
console.log("树的最小值",binarySearchTree.min());
// 测试获取最大值函数
console.log("树的最大值",binarySearchTree.max());
// 测试搜索节点函数
console.log("8在二叉树中",binarySearchTree.search(8));
console.log("100在二叉树中",binarySearchTree.search(100));
// 测试节点删除
console.log("删除节点3");
binarySearchTree.remove(3);
binarySearchTree.inOrderTraverse(printNode);
完整代码请移步: BinarySearchTreeTest.js
执行结果如下:


阅读量:2033
点赞量:0
收藏量:0
 小乔学算法
小乔学算法